Bayes

UFOs

(example taken from Kurt, 2019)

You are awakened by a bright light at your window.
You get out of bed and see a saucer-shaped object in the sky.
Although you don’t believe in aliens, you think to yourself “could this be a UFO?”

(example taken from Kurt, 2019)

“The probability of observing bright lights outside the window and a saucer-shaped object in the sky is very low.” Or:
- $P$(bright light outside your window, saucer-shaped object in the sky) = very low

The probability of observing bright lights and a saucer-shapd object in the sky, given our experience on Earth, is very low. Or:
- $P$(bright light outside your window, saucer-shaped object in the sky | our experience on earth) = very low
This is called a conditional probability; are conditioning the probabiltiy of one event occurring on something else.

Probability of hypothesis, given experience:
- $P(H_1 \mid X)$ = very, very low.
But what if $H_2$ = a film is being made outside your window?
- $P(H_1 \mid X)$ = very low.

(example taken from Kurt, 2019)

Perhaps we have a new hypothesis?

$P(D_{updated} \mid H_2, X) >> P(D_{updated} \mid H_1, X)$
The probability of the data, given the second hypothesis, is much greater than the first.

We can express the comparison of these two hypotheses as a ratio:

$\frac{P(D_{updated} \mid H_2, X)}{P(D_{updated} \mid H_1, X)}$

If this is a large number (like 1000), it means that $H_2$ explains the data 1,000 times better than $H_1$

(example taken from Kurt, 2019)

$P(H) = \frac{O{H}}{1 + O(H)}$
You give your friend 6:1 odds that Northwestern will beat Purdue in basketball. You’ll give your friend $30 if Purdue wins, he will only pay you $5 if Northwestern wins.
$P(NU Win) = \frac{O(NU Win)}{1 + O(NU Win)} = \frac{6}{7} = .857$
You are giving NU about an 86% chance of winning.

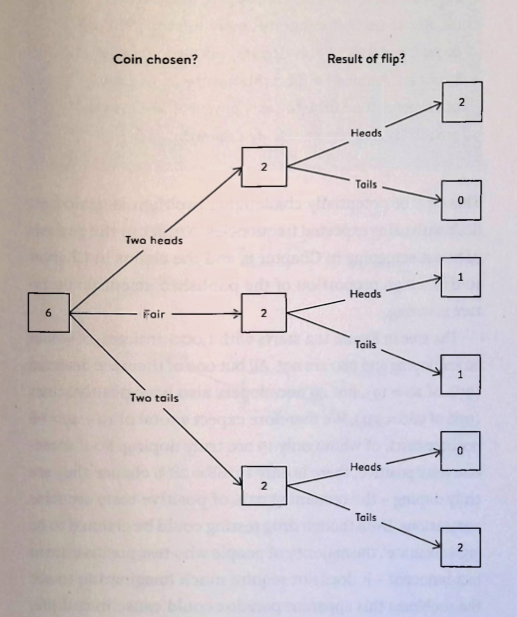
Spiegelhalter Coin Flip

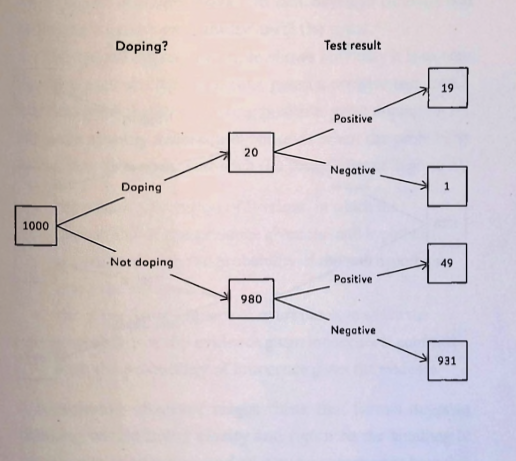
Spiegelhalter Doping

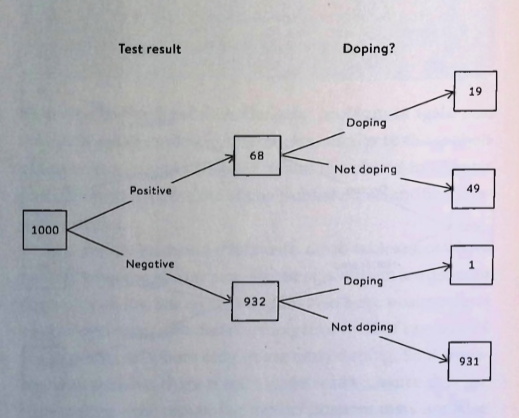
Spiegelhalter Doping

Richard III, who Shakespeare characterized as an evil hunchback, was said to have been buried in Greyfriars Priory in Leicester.

We might assume that a skeleton found were the remains of Richard the III if all of the following were true:

he had really been buried in Greyfriars
his body had not been dug up and moved or scattered in the intervening 527 years
the first skeleton found happened to be him.

Let’s say 50% chance the stories of his burial were true
Let’s say 50% chance that his skeleton is still where he was originally buried in Greyfriars
Imagine that up to 100 other bodies were also buried in this location.
1/2 * 1/2 * 10/100 = 1/400.

Spiegelhalter Richard III

Spiegelhalter Richard III

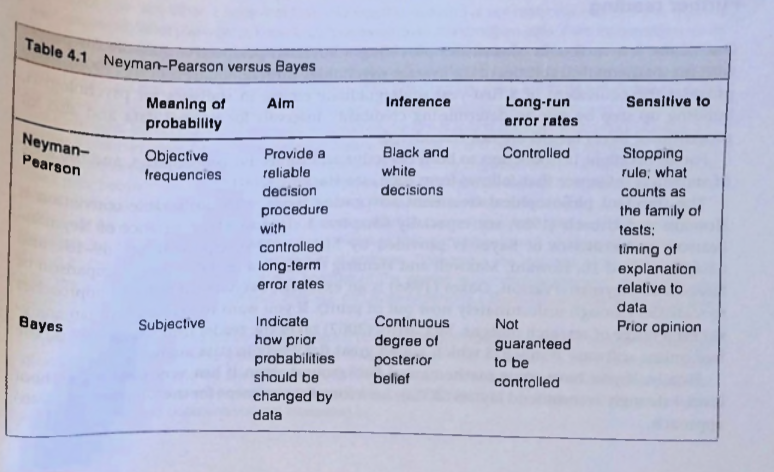
Dienes comparing methods